امروز قصد دارم مطالبی دیگر از کتاب افسون ریاضیاتبنویسم:
سابقه اعداد شمارشی به دوران ماقبل تاریخ باز میگردد و همچنین تمدنهای باستانی از وجود کمیتهای کسری آگاه بودند. مسئلهای که برام جالب بود این بود که اعداد منفی حتی تا قرن 16 میلادی کاملا پذیرفته نشده بود و اول بار اروپاییان از نوشتههای اعراب متوجه اعداد منفی شدند. میخایل اشتیفل( قرن شانزدهم) اعداد منفی را بی معنی و احمقانه میدانست، حتی بلز پاسکال گفته است:« من کسانی را میشناسم که نمیتوانند بفهمند با برداشتن چهار از صفر، صفر باقی میماند».
مردم دنیای باستان با نگاه به ستارگان و سیارهها و دانههای شن در ساحل ، مفهوم بی نهایت را احساس میکردند.
از آنجا که در تعالیم مذهبی استفاده از تصاویر حیوانات در هنر اسلامیممنوع بود، هنرمندان مسلمان مجبور به استفاده از ریاضیات به عنوان راهی برای بیان هنری تکیه شدند و این امر آنان را به خلق گنجینهای از طرحهای کاشی کاری رهنون شد.
هر سلول زندهای از شش عنصر بنیادی- کربن، هیدروژن، اکسیژن، فسفر، نیتروژن و گوگرد – تشکیل شده است. این اتمها در سلول با هم ترکیب میشوند تا ملکولهای آب ، فسفات و قند ساخته شوند.
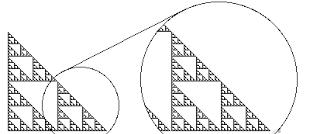
در ادامه به مبحثی نسبتاً جدید در ریاضیات به نام Fractal یا برخال اشاره میکنم:
هندسه اقلیدسی برای توصیف چیزهایی مانند بلورها و کندوهای عسل بی نظیر است. اما انسان در یافتن اشکالی در هندسه اقلیدسی برای شکل ذرت بو داده، اشیای خشک شده، پوست درختان، ابرها، ریشه زنجبیل و خطهای ساحلی به سختی در مضیقه قرار میگیرد. با معرفی فضای فراکتالی در 1975 توسط ماندل برو در این زمینهها میتوان توصیفی ارائه کرد.
فرض کنید میخواهیم مسافت خط ساحلی را اندازه بگیریم میدانیم در ریاضیات فاصله را میتوان با هر واحدی اندازه گرفت- مثلا متر، سانتی متر، میلی مترو ...- بدون توجه به واحد اندازه گیری مسافت بدست آمده یکسان خواهد بود. حال اگر خط ساحلی را دارای ماهیتی فراکتالی بدانیم آنگاه پاسخها یکی نخواهند بود و هرچه واحد اندازه گیری کوچکتر باشد قادر خواهیم بود که شاخابهها و خلیجهای بیشتری از خط ساحلی را اندازه گیری کنیم. خط ساحلی در هندسه برخالی دارای طول بی نهایت میباشد.
در اشکال فراکتالی هر جزء کوچک شبیه کل شکل میباشد. نمونههایی از این اشکال در زیر نشان داده میشوند.